Motivation

The cartpole is one of my favorite mechanical systems. Very few systems of such simplicity produce the predictable chaos that is visually interesting. Something about the movement of the cartpole seems natural. Even though most of us have never played with a cartpole before, it seems somehow familiar. Understanding how to control a cartpole is fundamental to some basic human skill, maybe riding a bike.

The cartpole is a single inverted pendulum attached to a mass with no friction constrained in movement to the axis perpendicular to gravity. A free body diagram of the system is shown below.

The simplicity of the cartpole made it the perfect system for me to learn new methods of control on. Whenever I try to implement a controller on a more complex system I make it work on the cartpole first. Here I will compare many methods of control including LQR, energy shaping, MPC and reinforcement learning.

Dynamics

Every good controls projects starts with the dynamics. Here I won’t derive the dynamics. I will instead link two excellent websites: Matthew Peter Kelly’s personal blog and Prof. Russ Tedrake’s textbook/course/website. I feel like these two resources have been instrumental in my interest in control. Here Matthew Peter Kelly derives the dynamics using rigid body kinematics, while here Prof. Russ Tedrake uses the Lagrangian. These both yield the same for the dynamics. They can be found in the code for this project. We use Matlab autogen functions to convert these dynamics into a state space equation of the form.

\[\dot{x} = f(x) + g(x)u\]

Where the state can be described by

\[x = \begin{Bmatrix} x\\ \dot{x} \end{Bmatrix}\]

First to build some intuition here is a GIF of the system showing a sinusoidal force being applied. Our goals in preforming control on this cart pole are to 1. stabilize it at its top point and 2. to dynamically flip it up to it’s top point.

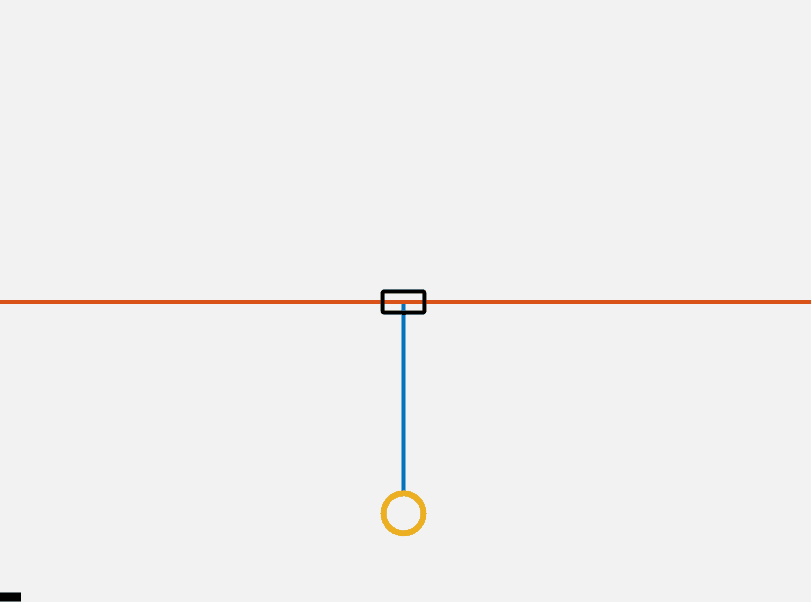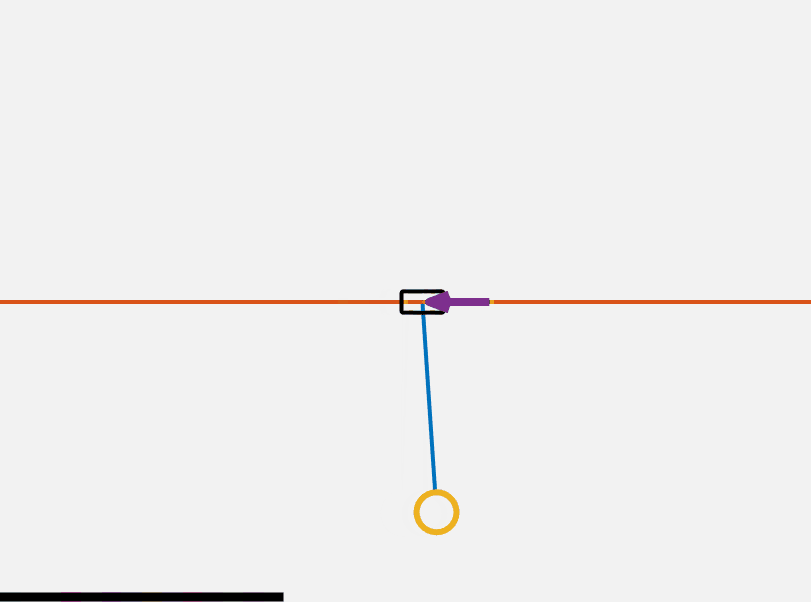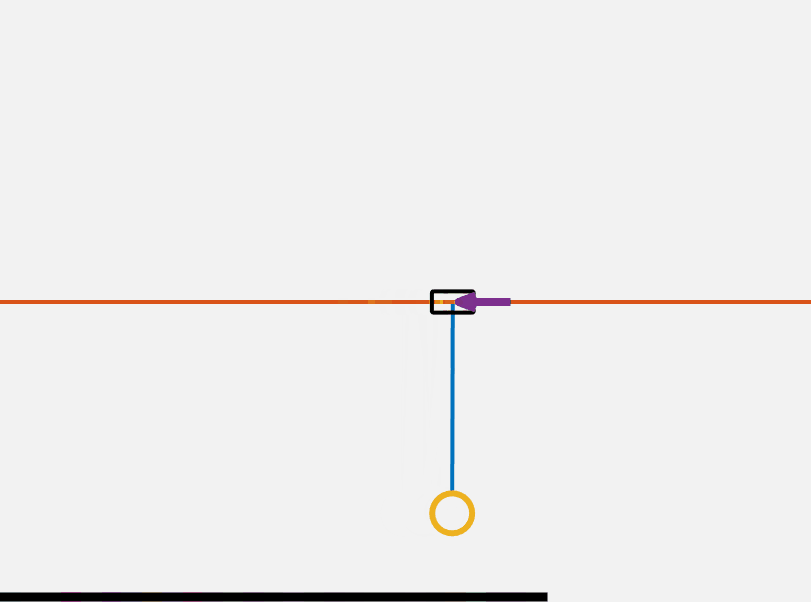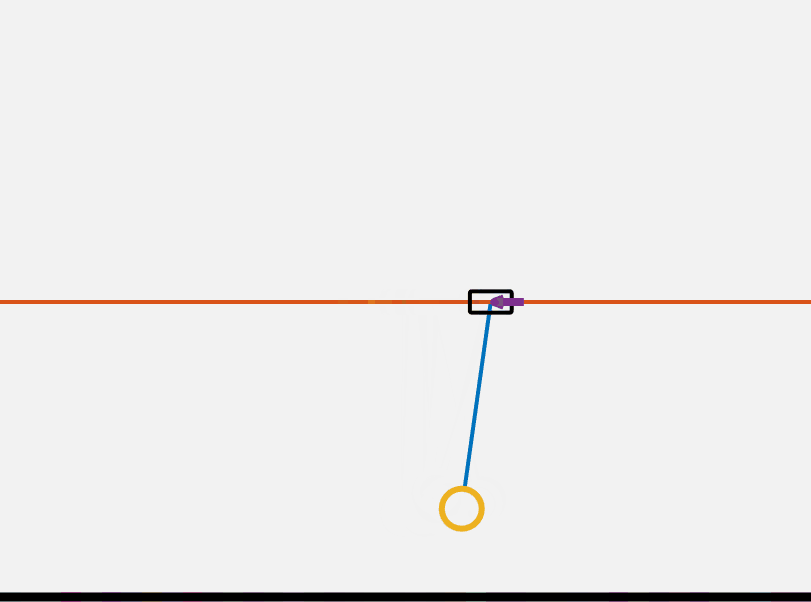
Control

First I build a simple linear controller which drives the cartpole state to 0. To do this I use a linear quadratic regulator (LQR) controller. An LQR controller minimizes the quadratic cost defined as

\[J = x^T(t_1)F(t_1)x(t_1) + \int\limits_{t_0}^{t_1} \left( x^T Q x + u^T R u + 2 x^T N u \right) dt\]

A controller u = -Kx can be solved for using the continuous time algebraic Riccati equation (CARE). For our purposes we use Matlab built in functions to solve this equation given our system dynamics. Below you can see that our system is surprisingly stable around the top equilibrium point.

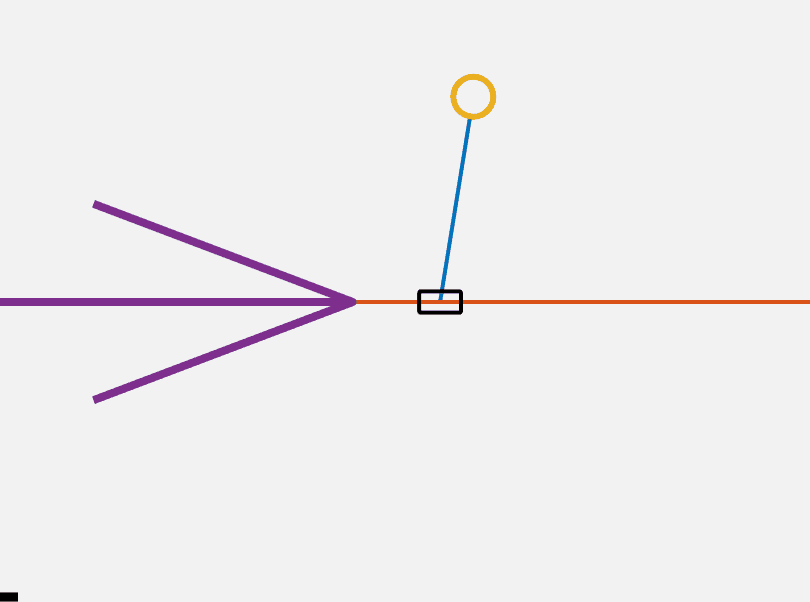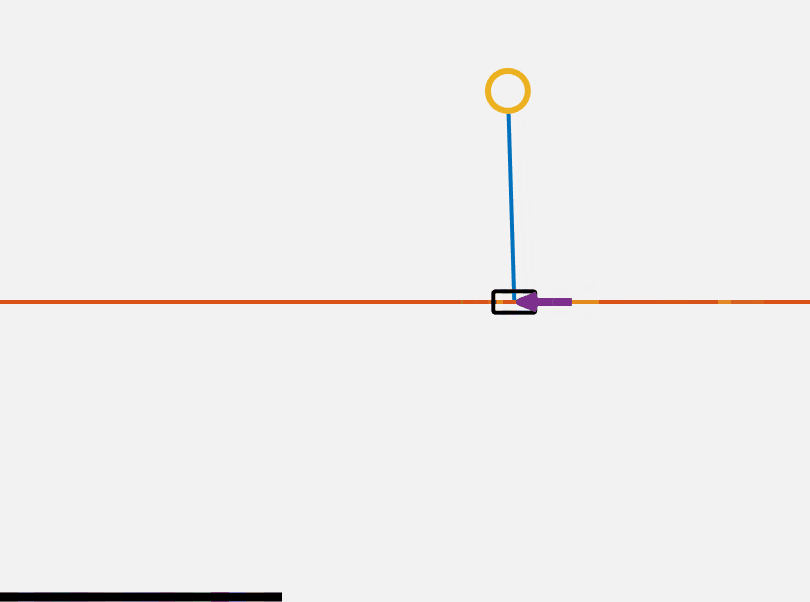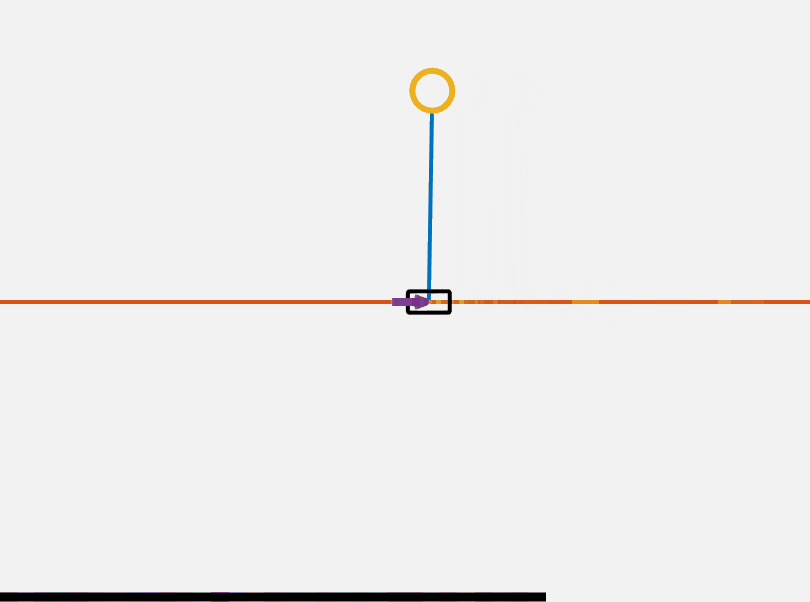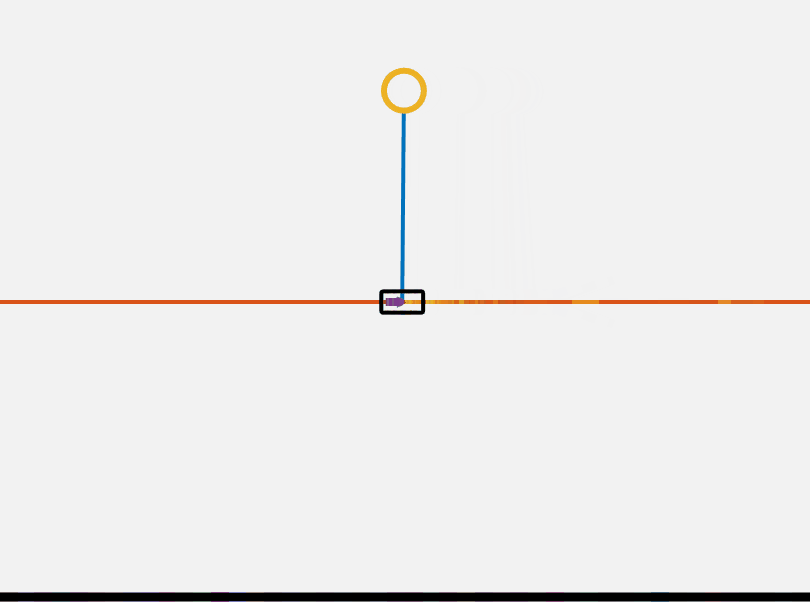
However, we still need to find a method to flip our cartpole up. We will do this using a method called energy shaping. We know the potential energy of the system is maximized when the pendulum is on the top of the cart. Therefore if we can design a controller which adds to the energy of the system we can flip the pendulum up. Our controller also needs to add to the energy of theta rather than x. We want to flip the pendulum up, not accelerate it to an infinitely high speed. Our controller thus has a dependance on the current angle.

\[u(t) = k (U(x)-U(x_{des})) \dot{\theta} \cos{\theta}\]

We saturate the input to be inside a reasonable value. Using this controller we can get the pendulum into the ballpark of the top. We can then switch to the LQR controller to stabilize at the top. This is shown below. One additional thing to note is that we could more rigorously certify that this controller is stable using Lyapunov analysis, which I made add in a future version of this post.

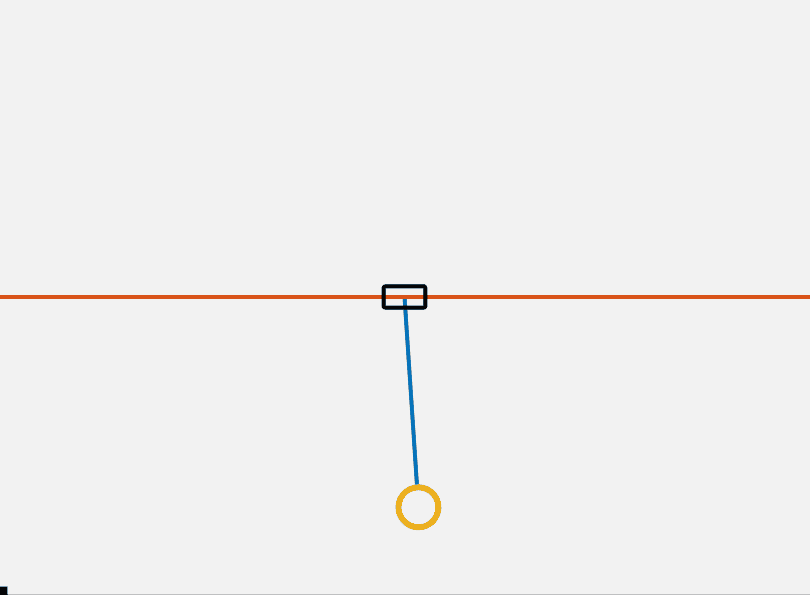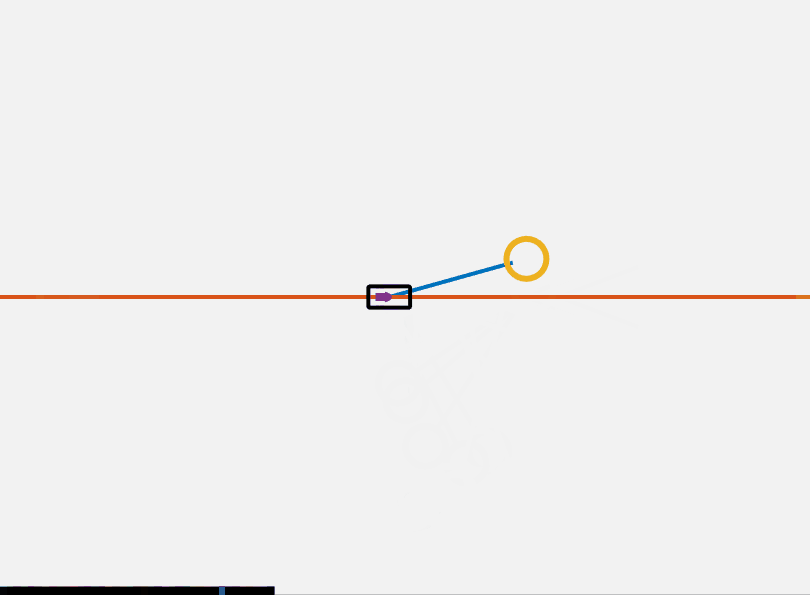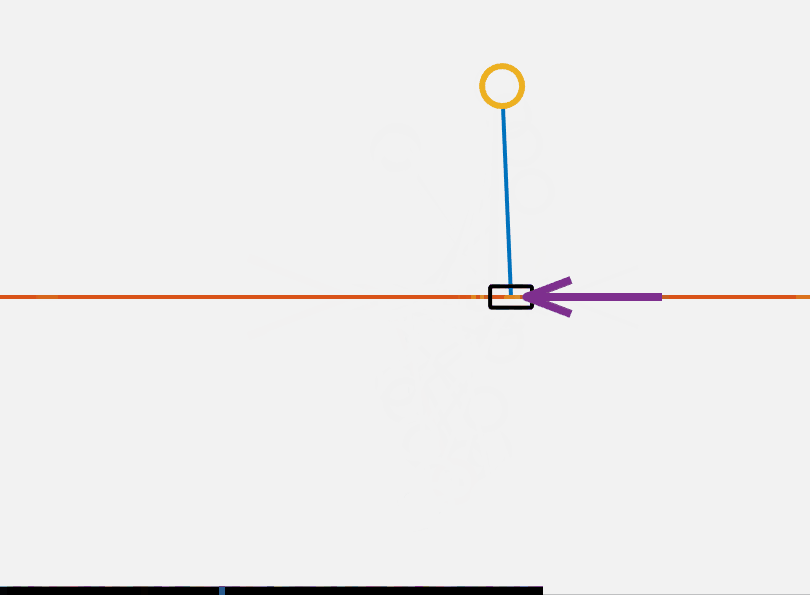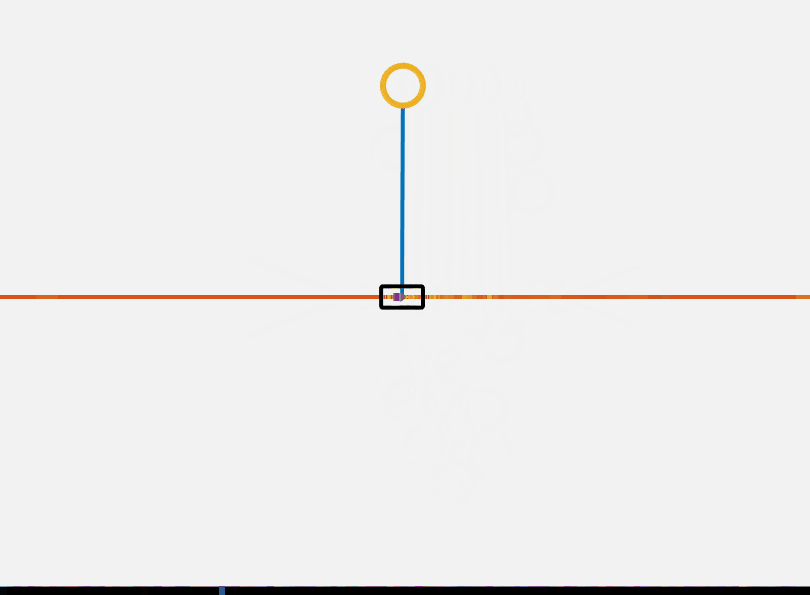
This controller has several major flaws. One of which is that this controller does not work for all initial conditions. If theta is equal to 0 the controller is at a singularity. This is an implication of the hairy ball theorem. No continuous controller can drive the system to a desired position.

We will now explore a new class of optimization based controllers. We will pose the problem of flipping the cart pole up as a nonlinear program. We wish to at every time step solve for the controller that minimizes the quadratic cost. Consider the following optimization based controller.

\[\begin{align} u^*=\underset{u \in \mathbb{R}^{m}}{\operatorname{argmin}} & ~ \sum_{k=0}^{N-1}(x^T_kQx)k+u_k^TRu_k)+x^T_{t+N}Q_Fx_{t+N}) \\ \mathrm{s.t.} & ~ x_{k+1} = Ax_k+Bu_k \nonumber\\ & ~ x_k \in \mathcal{X}, \; u_k \in \mathcal{U} \nonumber\\ & ~ x_1 =x(0), \; x_N \in \mathcal{X}_F \nonumber \end{align}\]

This controller solves for the optimal control input over a horizon of N steps with an initial and final condition subject to the linearized dynamics at each time step. By solving an optimization problem like this at each time step we can implement model predictive control (MPC). MPC generally requires more computational power than the simple controller presented above. Additionally, proving the stability of an MPC controller is fairly complicated. This MPC algorithm can be seen in action in the below GIF. I use CasADi to transcribe and solve the nlp.

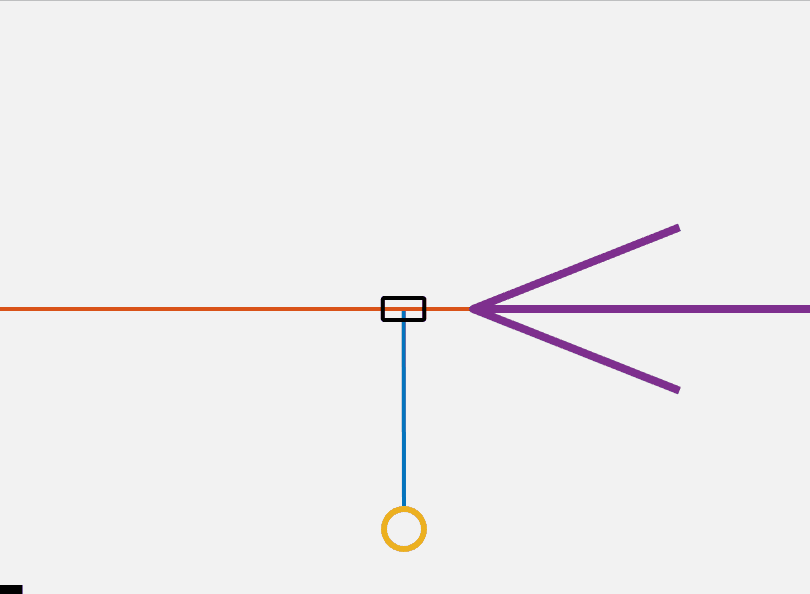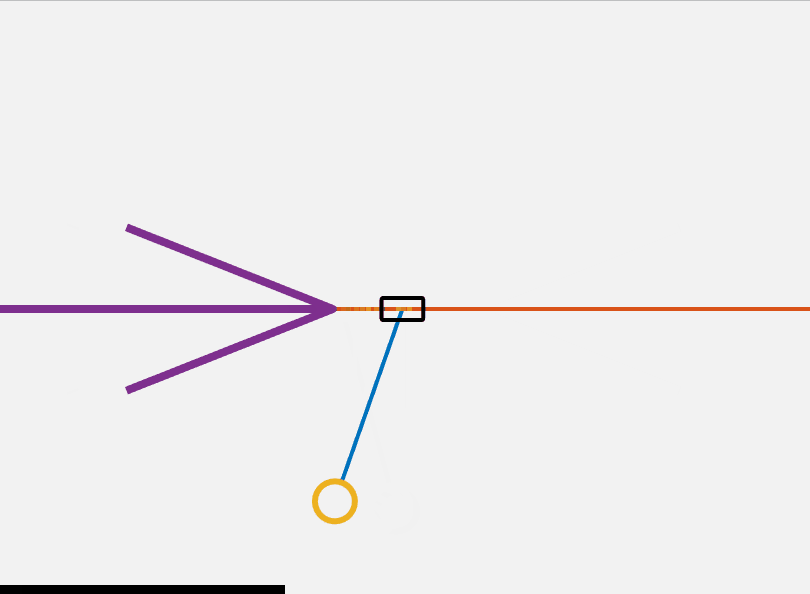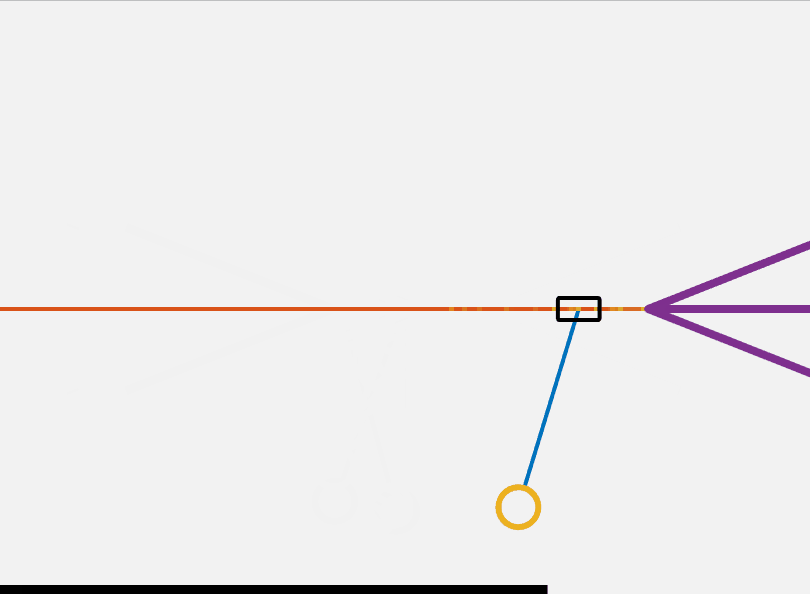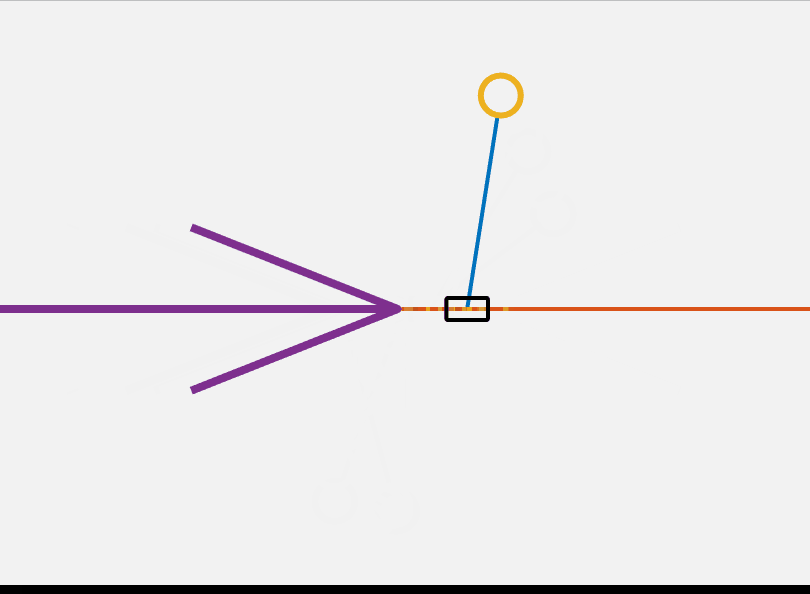
It is clear that the MPC controller takes a much more optimal approach to the flip up problem then the other algorithms discussed here. So far I have introduced the cartpole system and presented several methods by which it can be controlled. All the programming above was done in Matlab and can be found here

We will now experiment with a entirely different class of controller. reinforcement learning based controller. The basic premise of reinforcement learning is that we generate a large number of agents and evaluate their behavior based on a cumulative reward function. Over many iterations we can converge on a policy which maximizes the objective reward function. We will use Nvidia Isaac Gym to simulate our cartpole agents. Isaac Gym is an exciting new piece of software that allows RL training to be run completely on a GPU. Before ML training was done on the GPU, but was bottlenecked by physics simulations on the CPU. Isaac Gym allows us to do both on the GPU.

We can train a policy in 220 seconds which preforms well in a simulation. This is shown in the video below. Code for this RL based controller can be found here and closely follows based on an example from Nvidia.