Motivation

I have always been fascinated by mechanical calculators. From slide rules to the Curta calculator something about the mechanical action and the geometric intuition is highly compelling to me. One day I will certainly build a 1:1 scale model of a Curta mechanical calculator.

Recently I have begun to think more about the relationship between physics and math. This relationship, at least how it exists in the university pedagogy, is completely one sided. Math is used to solve physics problems, and never the other way around. But this doesn’t make any sense, nature is the ultimate calculator. It can solve NP hard problems like protein folding in nanoseconds. Why can’t we design physics experiments which solve our hardest math equations ?

I mostly am advocating for the concept of using physics to solve math. There are a number of problems to say solving the traveling salesman problem using protein folding. However I see one area in particular in which this could be applied. Gradient decent is the key to much of machine learning. A ball rolling down a hill is also gradient decent. Can we create a configurable optical gradient CPU. Something that would allow speed of light gradient decent. So we can solve directly for local or global minima of a complex function.

Quadratic Equation Slide Rule

How it Works

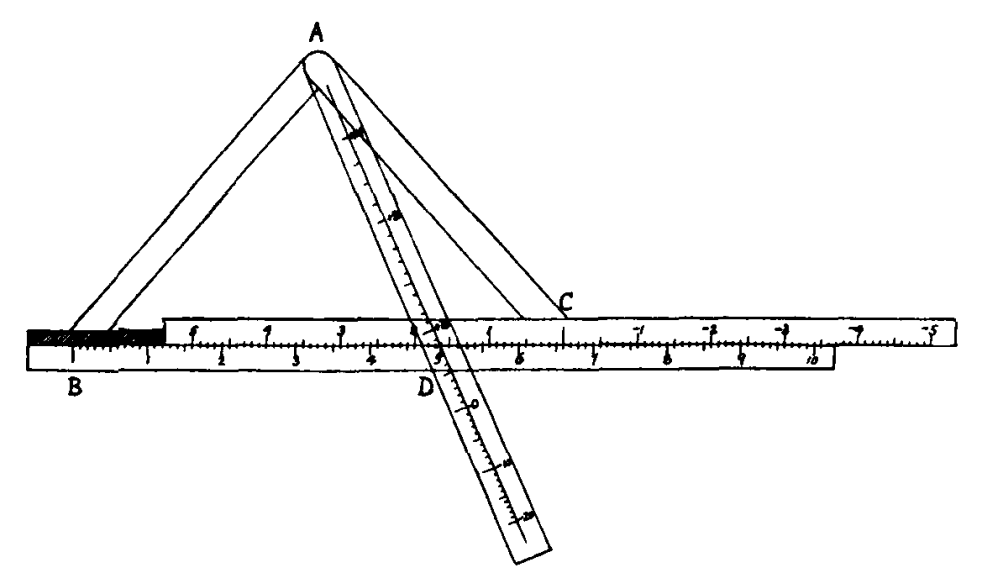
This quadratic equation solving slide rule is from a paper I found which was published in 1919 after the World War I. This slide rules uses the physical laws of 3D space to solve a form of the quadratic equation. Here is how it works:

Consider the above triangle. Assume that \(AB\) and \(AC\) are equal in length so that \(\triangle{ABC}\) is isosceles. We will now use the law of Cosines to develop a relationship between \(BD\), \(DC\) and \(AB\). Consider the following labeled edges and angles.

We will derive a special case of Stewart’s theorem using the law of cosines.

\[c^2 = m^2 + d^2 - 2dm\cos \theta\] \[b^2 = n^2 + d^2 - 2dn\cos \theta'\]

For our isosceles triangle \(c^2 = b^2\). We can also apply the property that \(\cos \theta' = -\cos \theta\) as \(\theta\) and \(\theta'\) are complementary angles. Thus

\[c^2 n = nm^2 + nd^2 - 2dmn\cos \theta\] \[b^2 m = mn^2 + md^2 + 2dnm\cos \theta\]

Adding the two equations and simplifying we get.

\[b^2(m+n)= mn^2 +nm^2 + md^2 +nd^2\] \[b^2 (m+n) = (m+n)(mn+d^2)\] \[mn = b^2 - d^2\]

We have now established the relationship that \(BD \cdot DC = AB^2 - AD^2\). We can preform the following substitutions to convert this into a quadratic equation. We substitute \(x\) for \(BD\), \(a\) for \(BC\), \(p\) for \(AB\) and \(r\) for \(AD\). We also substitute \(BC - BD = DC\). Thus,

\[x^2-ax + (p^2-r^2)\]

We now have a form of the quadratic equation that we can solve geometrically. I will now demonstrate the process with an example.

INSERT EXAMPLE HERE (need to buy adobe illustrator cannot keep using inkscape)

Making it Real (Coming soon)

I am in the process of designing an easy to manufacture open source version of this